PARTICULES ÉLÉMENTAIRES - Traitements statistiques en physique des particules

PARTICULES ÉLÉMENTAIRES - Traitements statistiques en physique des particules

En physique des particules, l’apparition des phénomènes (événements) est le plus souvent de nature aléatoire et les mesures sont toujours entachées d’erreurs, elles aussi aléatoires. Pour cette raison, il est impératif de faire appel à un traitement statistique de l’information: cf. détecteurs de PARTICULES (détecteurs à visualisation).

On décrira ici l’ensemble des traitements et on présentera l’analyse d’une expérience du point de vue de la statistique. On prendra pour exemple l’étude des clichés de chambre à bulles, qui montre bien la complexité des opérations nécessaires à l’analyse correcte d’une expérience.

Le cadre statistique le plus généralement utilisé est maintenant celui de la théorie de la vraisemblance. En effet, d’une part, sous certaines conditions, on peut montrer que l’estimation du maximum de vraisemblance est la meilleure, d’autre part, le postulat de Bayes permet de considérer la vraisemblance comme une probabilité, donc de traiter les résultats de l’expérience eux aussi dans un cadre probabiliste.

1. Les bases statistiques. Vraisemblance dans une expérience

Il faut d’abord définir les différentes variables entrant en jeu:

– Les variables mesurées E sont toutes les informations qui ont été recueillies, en particulier les coordonnées x et y de points des trajectoires des particules mesurées sur les clichés.

– Les variables définissant l’expérience D sont toutes les variables permettant de décrire de façon exhaustive ce qui s’est passé dans l’expérience. On peut citer le nombre de clichés (pour chaque cliché, le fait qu’il ait été ou non sélectionné et par qui), le nombre de particules entrantes, leurs caractéristiques, le nombre d’interactions, leur localisation dans la chambre à bulles, le nombre de particules sortantes, les caractéristiques de chacune d’elles et les trajectoires ou les interactions secondaires auxquelles elles donnent lieu. Ces variables sont, bien sûr, en nombre incroyablement élevé. En particulier le long de sa trajectoire, une particule rencontre un très grand nombre d’atomes et interagit avec eux, d’où des phénomènes de perte d’énergie et de déviation de la trajectoire, ou scattering .

– Les variables intéressantes R sont les variables que le physicien cherche à atteindre: la vie moyenne de telle particule, la fréquence d’apparition de telle résonance, de telle valeur de masse effective d’un ensemble de particules sortant, ou bien encore tel paramètre théorique dont dépend la fréquence d’apparition d’un type d’événements. Bien sûr, ces variables R peuvent aussi être des variables D. Elles peuvent également être des paramètres entrant en jeu dans des lois de probabilité ou même, à la limite, être elles-mêmes des fonctions inconnues.

2. Vraisemblance des variables R

La probabilité d’avoir obtenu et mesuré les éléments de l’expérience peut s’écrire:

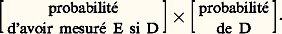La vraisemblance de R est l’intégrale de cette probabilité sur toutes les valeurs de D permettant la réalisation de R, ce qui peut s’écrire symboliquement:

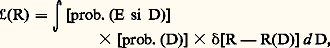où R(D) est la valeur de R fonction des variables D et où 嗀 est la «fonction de Dirac»: cf. DISTRIBUTIONS (mathématiques).

Toute l’information que l’on peut extraire de l’expérience sur les variables R est contenue dans 硫(R) et, en un sens, tout le travail d’analyse se résume à évaluer le mieux possible cette intégrale à un nombre incroyablement élevé de dimensions.

Pour calculer cette intégrale, il est nécessaire, d’une part, de faire des approximations et, d’autre part, d’utiliser toutes les particularités qu’elle peut présenter, parmi lesquelles on peut citer les possibilités de factorisation, donc d’intégration partielle plus aisée.

La première propriété intéressante est que 硫(R) est un produit de termes dont chacun représente la contribution d’un cliché. On peut même grouper à part les contributions de tous les clichés où aucun événement n’a été trouvé: ils interviennent de façon très simple dans 硫(R). En s’intéressant ainsi au fait qu’un événement a été ou non trouvé dans un cliché, on rencontre le premier problème spécifique de l’analyse: l’efficacité du dépouillement.

Une autre propriété importante vient du fait que, pour les variables R généralement utilisées, on peut trouver des ensembles de variables intermédiaires I, dont la connaissance suffit à déterminer R.

Soit, par exemple, le schéma suivant:

Variables mesurées x ^m de vraies valeurs x ^v , probabilité de mesure P (x ^m si x ^v );

x ^v = x ^v ( ¹, a ¹), où les a ¹ sont aléatoires: loi de probabilité Q¹ (a ¹ si Q);

¹ = ¹( ², a ²): loi de probabilité de a ², Q²(a ² si ²);

x ^v sont des variables E (de réalisation x ^m ) et ², a ², a ¹ sont des variables D;

¹ variable I;

² variable R.

On peut écrire la vraisemblance de ²:

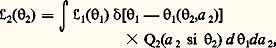où: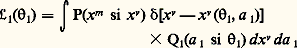

est en fait la vraisemblance des ¹ que l’on considère ensuite comme des variables E.

C’est cette propriété qui va permettre de distinguer plusieurs étapes dans l’étude d’un cliché. Leur nombre et leur définition dépendent des méthodes d’analyse adoptées dans les divers laboratoires; ainsi, pour les chambres à bulles à liquide lourd, la tendance est de considérer trois étapes:

– reconstruction des trajectoires des particules dans l’espace;

– détermination des paramètres des trajectoires au niveau de l’interaction primaire;

– détermination des caractéristiques de l’interaction.

On regroupe quelquefois les deux premières phases sous le nom de géométrie, la dernière phase étant appelée cinématique. Ces terminologies sont d’ailleurs un peu impropres, car la deuxième étape peut faire intervenir la masse de la particule, paramètre cinématique, la dernière phase pouvant faire aussi entrer en jeu des paramètres géométriques comme la position d’un vertex d’interaction reconstruit à partir des trajectoires.

En fait, d’un point de vue statistique, il est plus important de souligner que les deux premières phases ne font intervenir à la fois qu’une seule particule, la troisième étant réservée à l’étude globale des particules de l’expérience.

Méthodes d’approximation

Même réduit à un seul cliché ou séparé en trois étapes, le calcul à effectuer est encore très compliqué, et il est nécessaire d’effectuer des approximations, d’une part à cause du trop grand nombre de variables, d’autre part à cause de la complication des lois ou même de leur non-connaissance relative. Ces approximations sont fondées sur le fait que les lois de probabilité mises en jeu sont généralement assez proches de la loi de Gauss et que les dépendances des variables E et R vis-à-vis des variables D sont approximativement linéaires.

On peut alors écrire:

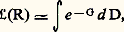où G est une fonction de D approximativement quadratique, et l’on sait que la valeur de cette intégrale sera:

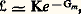où G^m est le minimum de G et où K est une fonction simple des dérivées secondes de G.

On voit donc que l’on peut remplacer le problème de calcul de 硫 par celui de la recherche du minimum de G, ou ajustement paramétrique (fit ); les valeurs rendant G minimal sont les valeurs qu’on estime les meilleures, les dérivées secondes de G fournissant une estimation des erreurs. G est une variable aléatoire (appelée 﨑²) et obéit donc à la loi de Pearson, ce qui permet de contrôler la qualité de l’information. L’avantage de la vraisemblance est qu’elle permet (par le calcul du facteur K) de comparer entre elles plusieurs hypothèses a priori possibles. On reviendra sur ce point dans les applications.

Dans certains cas, on est obligé de faire ce que l’on appelle des coupures , c’est-à-dire de rejeter des événements ne satisfaisant pas à certains critères; par exemple, on peut exiger que le 﨑² ait une valeur suffisamment petite. Ces événements ainsi rejetés sont pour la plupart des événements ayant plusieurs interprétations possibles, et il peut être difficile d’évaluer correctement la probabilité de ces hypothèses ou même de les recenser, c’est-à-dire que l’on ne peut connaître suffisamment bien la contribution apportée par l’événement à 硫(R). En général, cette contribution est de plus assez faible.

Une telle technique de coupure revient à limiter les volumes d’intégration des intégrales d’une manière que les méthodes d’intégration ne pourront parfois pas facilement contrôler.

3. Application à l’analyse

Efficacité de dépouillement

La recherche dans un ensemble de clichés des «événements intéressants» est un travail long et difficile (il faut regarder plusieurs centaines de milliers de photographies); il est donc très rare que tous les événements soient notés au dépouillement. En effet, d’une part, l’attention du personnel n’est pas parfaite, d’autre part, certains événements, de par leur configuration et leur situation dans la chambre, sont plus difficiles à apercevoir. Il est facile de corriger les effets de l’inattention des dépouilleurs en supposant que tous les événements ont la même probabilité d’être observés. Pour connaître cette probabilité, il est nécessaire d’effectuer un second dépouillement au moins partiel. En notant les événements qui ont été vus au premier, au second ou aux deux dépouillements, on peut calculer l’efficacité du dépouillement et ainsi estimer le nombre d’événements réellement produits lors de l’expérience.

Reconstruction des trajectoires dans l’espace

Il s’agit, étant donné un ensemble stéréoscopique de photographies d’un événement, de reconstituer dans l’espace les trajectoires des particules. La première phase consiste à mesurer, à l’aide d’un appareil plus ou moins automatisé, un certain nombre de points de l’image de la trajectoire de chaque trace. La trajectoire d’une particule en présence d’un champ magnétique est très proche d’une portion d’hélice dont la courbure dépend de l’impulsion de la particule. On peut donc chercher à trouver une hélice telle que ces images soient le plus près possible des points mesurés, c’est-à-dire que l’on fait une estimation par ajustement paramétrique de manière à rendre minimale la somme des carrés des distances des points mesurés aux images de l’hélice.

En fait, comme on le verra ci-dessous, la trajectoire n’est pas une hélice et l’estimation précédente ne peut se faire que sur une petite portion de la trajectoire. Il faut donc découper chaque trajectoire en petits segments d’hélice. Le résultat en est un ensemble de points dans l’espace (et éventuellement de directions et de courbures) par où est passée la particule, aux erreurs de mesures près, erreurs que l’on évalue évidemment.

Dans le cas d’événements assez compliqués, cette partie de calcul est rendue difficile par le fait qu’on ne sait pas toujours identifier les images d’une même trajectoire sur des photographies différentes du même événement. On doit donc ajouter une étape préliminaire pour chercher quelle est la bonne identification. Cela ne peut d’ailleurs se faire que si l’on a à sa disposition au moins trois vues de l’événement, la troisième servant à vérifier le choix fait sur les deux premières. Tous les calculs sont faits par un ordinateur, le temps de calcul nécessaire à cette reconstruction étant de 1 à 5 p. 100 du temps total utilisé pour analyser l’expérience.

Détermination des paramètres de la trajectoire

Les paramètres à déterminer sont la position ぬ et l’impulsion ら de la particule au début de sa trajectoire. Les points dans l’espace déterminés par l’étape précédente constituent les mesures. La trajectoire de la particule dépend non seulement de ぬ et de ら, mais encore de toutes les interactions avec les constituants du liquide rencontrés par la particule.

Comme ces interactions ne font pas en général partie des variables R, on doit les intégrer sur toutes les variables les décrivant. Cela peut se faire à l’aide des méthodes décrites plus haut. Le résultat est que l’on peut utiliser non pas la trajectoire réelle, mais une trajectoire idéale, la trajectoire moyenne ayant les mêmes paramètres initiaux ぬ et ら. On doit de plus ajouter aux erreurs de mesures, relatives à l’étape précédente, des erreurs dues aux incertitudes sur les phénomènes d’interaction avec le liquide. Le calcul de la vraisemblance, qui est ici 硫(face="EU Arrow" ぬ, ら), revient alors à l’estimation de la trajectoire passant le plus près des points mesurés, compte tenu de l’ensemble des erreurs.

En réalité, la trajectoire dépend aussi de la masse, et la comparaison des vraisemblances dans les diverses hypothèses de masses possibles permet d’avoir des indications sur la valeur de la masse de la particule.

Dans le cas des électrons, en plus de la perte d’énergie par ionisation et des déviations dues au scattering comme pour toutes les particules, intervient une perte d’énergie par rayonnement suivant une réaction du type:

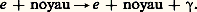Malheureusement, les lois de probabilité gouvernant ce type de perte d’énergie sont très loin de ressembler à des lois de Gauss. Il est donc nécessaire d’utiliser pour l’électron des méthodes spéciales pouvant conduire, par exemple, à des intégrations numériques. Le temps de calcul nécessaire à cette étape est, lui aussi, d’environ 5 p. 100 du temps total.

Détermination des caractéristiques de l’interaction

On dispose maintenant pour une interaction des impulsions ら et éventuellement des masses des particules sortantes observées sur le cliché. Le problème est de déterminer les caractéristiques de l’interaction. Cela se fait la plupart du temps, comme dans les étapes précédentes, à l’aide d’un ajustement paramétrique, mais ici, dans certains cas, les limitations cinématiques interdisent d’utiliser les méthodes d’approximation (la dépendance des variables E ou R, vis-à-vis des variables D, n’est plus linéaire), et l’on doit recourir à des méthodes d’intégration directes, par exemple numériques.

Cependant, le problème le plus important dans cette étape est qu’il faut souvent choisir entre deux interprétations possibles de la même interaction. Voici trois exemples:

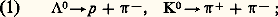ces réactions, où le 炙 et le K ne sont pas visibles, donnent naissance à des configurations topologiques semblables; si, de plus, la trajectoire positive ne permet pas d’identifier sûrement la masse, les deux interprétations devront être considérées:

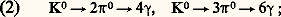ces deux réactions auront des configurations identiques si deux des 塚 de la seconde réaction ne se matérialisent pas en paire e⁺ e ^- à l’intérieur de la chambre:

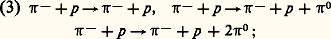ces trois réactions ont encore une fois des configurations topologiques semblables si les 神⁰ ne sont pas visibles, comme il est fréquent dans une chambre à bulles à hydrogène.

Une méthode consiste à rejeter comme fausses les hypothèses ayant, lors de l’ajustement cinématique un 﨑² trop grand. Il peut rester cependant une proportion assez élevée de cas ambigus, c’est-à-dire pour lesquels plusieurs hypothèses sont acceptables. Le calcul de la vraisemblance des hypothèses permet alors de pondérer chacune d’entre elles dans l’analyse finale. Cette étape peut utiliser de 10 à 20 p. 100 du temps de calcul.

Analyse finale

Une fois chaque événement étudié, on rassemble leur contribution pour calculer la fonction 硫(R) qui donne le résultat. En particulier, son maximum fournit l’estimation des variables R.

La façon de présenter les résultats peut alors varier d’une expérience à l’autre:

– Si un grand nombre d’événements entrent en jeu, 硫(R) aura la forme d’une fonction de Gauss, et l’on pourra publier l’estimation et l’erreur.

– S’il y a peu d’événements, on essaiera plutôt de présenter des intervalles de confiance, ou bien on publiera une représentation graphique de 硫(R) lorsqu’il y a une ou deux variables R seulement.

Un autre point à considérer est le nombre de variables R.

Dans les expériences à substrat théorique important, c’est-à-dire sur des sujets où la théorie est bien développée, le nombre des variables R est faible (quelquefois égal à 1). Au contraire, si le substrat théorique est faible, le nombre de variables est important; on peut même vouloir déterminer une fonction inconnue, par exemple un spectre de masse. Il faut un nombre infini de mesures pour déterminer une fonction inconnue; on se borne à chercher à déterminer l’intégrale de la fonction dans des intervalles limités. On est donc amené à publier des histogrammes (fig. 1 et 2) qui permettent de se faire une idée de la variation des fonctions inconnues. Le temps de calcul nécessité est de l’ordre de 10 à 30 p. 100.

Simulation de l’expérience (techniques de Monte-Carlo)

La simulation de l’expérience, presque inexistante vers 1960, a pris un développement rapide et important puisqu’elle peut nécessiter actuellement jusqu’à 50 p. 100 du temps de calcul. Elle répond essentiellement à deux objectifs: contrôler les approximations faites lors de l’analyse et calculer un certain nombre de fonctions, en particulier le pouvoir analyseur, ou fonction de détection de l’appareillage utilisé.

Si l’on suppose connues les lois d’apparition des événements que l’on étudie, cela consiste à simuler entièrement l’expérience sur ordinateur. On crée ainsi des événements dits de Monte-Carlo (en général plus nombreux que les événements expérimentaux). On leur fait subir le même traitement d’analyse qu’aux événements expérimentaux. La comparaison des deux séries de résultats permet alors d’atteindre les objectifs fixés. Cette partie d’analyse étant très coûteuse en temps de calcul ainsi qu’en travail pour les analystes, et chaque cas étant un peu un cas d’espèce, on utilise en général des techniques permettant de simplifier le processus.

À cause du fractionnement de l’analyse en plusieurs phases, on peut éviter d’avoir à restituer l’événement dans ses moindres détails. On créera, par exemple, des points dans l’espace sur les trajectoires des particules, mais on ne cherchera pas leurs images sur les différentes vues; on économisera ainsi cette partie de calcul, de même que la seconde phase de l’analyse. Plus généralement, à chaque partie que nous avons décrite correspond un minimum de simulation que l’on peut ne pas chercher à dépasser.

On peut faire l’économie d’une partie de la simulation en utilisant des événements voisins, si l’on veut, par exemple, étudier la réaction:

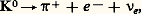où les K⁰ sont produits par la réaction:

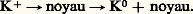Toute la partie de production du K⁰ peut être simulée par l’étude des événements de type voisin K⁰神⁺ 神^-, ce qui évite l’utilisation de modèles compliqués et hasardeux pour décrire l’échange de charge K⁺K⁰.

L’analyse d’une expérience est donc une chose difficile; elle nécessite des développements théoriques importants et beaucoup de temps pour les physiciens chargés de l’analyse (de un à cinq ans). Enfin, elle fait appel à des techniques de calcul très élaborées.

On peut estimer que le coût total en temps de calcul doit être de l’ordre de mille heures sur les plus gros ordinateurs existants. Cela correspond à environ une demi-heure de calcul par heure de fonctionnement de l’accélérateur. Ce dernier chiffre est aussi à peu près valable pour les expériences de compteurs ou de chambres à étincelles.

Encyclopédie Universelle. 2012.